久々に本棚を整理していたら、懐かしいものが出てきました。その名も「課題研究論文集」。管理人が高校時代に行った課題研究の成果を綴った論文(10ページほどですが)が収録されている代物です。
管理人チームの研究テーマはずばり「ジャイアンの声でガラスは割れるのか?」。実に空想科学読本に出てきそうなテーマ(実際にある)なのですが、それを真面目に検証しようということです。全国大会でも発表したので、もしかしたら知っている方もいるかもしれません。
今回はその研究の内容について、細かい部分は端折って紹介しようと思います。
※当時の論文の内容とは少し異なります。
ジャイアンの声でガラスは割れるのか?
どんな研究?
国民的アニメ「ドラえもん」では、ジャイアンの歌声で窓ガラスが割れる描写があります。管理人チームは、現実でもそのようなことが可能かどうかに興味を持ち、「共振」という現象を用いてガラスの振動の様子を調べることにしました。
共振とは
共振(きょうしん)は、エネルギーを有する系が外部から与えられた刺激により固有振動を起こすことである。特に、外部からの刺激が固有振動数に近い状態を表す。共鳴と同じ原理に基づく現象であるが、電気や固体については「共振」の語がよく用いられる。
Wikipediaより
物質はそれぞれ「固有振動数」という振動数をもっており、これに近い値で振動させることで「共振」が起こって激しく振動させることができます。その「共振」を利用してガラスを割っていこうという算段です。
以下の動画では、ワイングラスを声で共振させて割ることに成功しています。他にも同様の動画がいくつかアップロードされています。
とりあえずワイングラス割ってみようか
上記のように、共振を使えばワイングラスは割れることがわかりました。管理人チームの誰一人として声でワイングラスを割ることはできないので、道具を使ってワイングラスを割っていくことに。ワイングラスはどうせ割るのでダイソーの安いものを大量に用意しましたが、今考えたらそんなにいらなかったと思います。割るのは楽しかったです。



濡れた指でワイングラスの縁をこする(ワインハープ)と音が出るので、その周波数をオシロスコープで測定します。これがワイングラスの固有振動数(の一つ)になります。その固有振動数と同じ周波数の音を低周波発信器で発生させ、スピーカーでワイングラスに当ててやると共振します。
また、弦の固有振動でもそうですが、測定して得られた固有振動数の倍音・三倍音等でも共振させることができます。

結構簡単に割れました。せっかくなので割れるグラスは全部割りました。
また、タイトル回収のためにジャイアンの声でも実験を行いました。「ジャイアンにボエボエ」という曲をそのままかけても共振が起こらず割れないのですが、一部をサンプリングして繰り返してやると低周波発信器のときと同様に割れました。
窓ガラスを音で割りたい
無事ワイングラスを共振で割ることに成功しましたが、これは再現実験にすぎません。ここからが本題で、窓ガラスに使用される正方形ガラスを共振させて割っていくことにしました。
ガラス板の共振
最初の動画のように、ワイングラスの場合は中にストローを挿すことで共振の様子を確認することができます。ガラス板の場合は共振現象によって発生する模様「クラドニ図形」を利用して固有振動数を測定します。
クラドニ図形(Chladni figure)は、ドイツの物理学者エルンスト・クラドニの名にちなんだ図形であり、物体の固有振動の節を可視化する方法である。
Wikipediaより

今回は、ガラスの上に塩を撒いてクラドニ図形を出現させました。この図形が表れているときに物体は共振していると言えます。ちなみにこの図形は数式化することができ、上記の図形の場合は
$$ z = \cos 2\pi x\cos 2\pi y$$
で表すことができます。3次元グラフにするとこんな感じ。
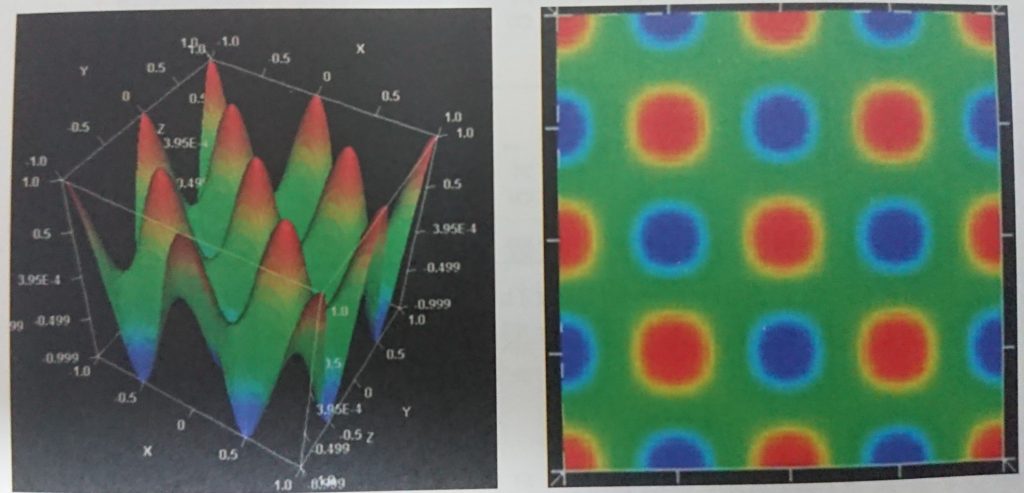
赤い部分と青い部分が振動の「腹」、緑の部分が振動の「節」の部分となり、この節の部分に塩が集まることでクラドニ図形が浮かび上がります。今回の研究では12種類のクラドニ図形を観測することができました。
実験
ワイングラスのときと同様の機材を使用して実験を行いました。スピーカーとガラスの距離は1mm、ガラスは四隅をスポンジ台に乗せています(ガラスを支える方法で固有振動数に影響が出ないのは確認済み)。スピーカーからは110dB程度(車直前でのクラクションくらい)の爆音で125-7000Hzの音波を発生させ、クラドニ図形が発生する(=共振する)周波数を探します。
正方形ガラスは厚さ 1, 2, 3, 4mmの4種類・辺の長さ150, 300, 450, 600mmの4種類の計16種類を用意しました。(結果には残していませんが、円形ガラスや長方形ガラス、もっと小さい・もっと厚いガラスも買ったので30000円弱かかったと思います。)
結果・考察
端折りますが、結果から言うとどの条件でもガラスは割れませんでした。
一方で、正方形ガラスの固有振動数 f [Hz]と厚さ t [mm]・辺の長さ L [mm]・固有値 λ との関係性を導くことができました。固有値とはクラドニ図形の模様によって決まる値で、例えば上記の模様の場合は8π2になります。(固有振動数 f [Hz],厚さ t [mm],辺の長さ L [mm],固有値 λ,比例定数 k [Hz*mm])
$$ f = k\lambda \frac{t}{L^2} $$
ちなみに、これは空想科学読本に書かれていた「窓ガラスの固有振動数は辺の長さに反比例する」という仮説への反証となります。
また、共振している正方形ガラスは各質点において単振動しているとみなせるため、以下の単振動エネルギーの式が成り立ちます。(エネルギー E [J],質量 m [kg],周波数 f [Hz],振幅 A [m])
$$ E = 2\pi^2 mf^2 A^2 $$
単振動エネルギーの式より、ガラスを小さく薄くして質量を小さくしたり、音量を上げてエネルギーを大きくしたりすることで、振幅Aが大きくなりガラスが割れやすくなると考えられます。実験においてもガラスが小さく薄いほど・音量が大きいほど激しく振動しました。
結論
ジャイアンが声で窓ガラスを割るためには、固有振動数の式 $ f = k\lambda \frac{t}{L^2} $ を満たす周波数の音を発生させ、単振動エネルギーの式 $ E = 2\pi^2 mf^2 A^2 $ を可能な限り大きくする必要がある。
おわりに
課題研究「ジャイアンの声でガラスは割れるのか?」の紹介でした。
当時は自分でもなかなかの出来だと思っていたので、全国大会行きが決まったときはとても嬉しかったです。ですが、今見返してみると論文は突っ込みどころ満載な気がします(笑)当時の自分に突っ込みを入れにいきたいくらいです。
当時は、部活にも行かず毎日残って研究をしていました。今考えるとさすがに部活に行く時間もとるべきだったと反省しております。今も研究を優先してサークル活動をおざなりにしている状況です。反省していません。
それでは、みなさんもよい研究ライフを。




コメント
わかりやすかったです‼(‘ω’)ノ
( ..)φメモメモ
確かに❕